
The mere mention of math can bring back haunting memories of unfinished exams and complex equations. But what if I told you that the math we’re about to explore confirms a lot of what you already intuitively know about SEO?
As SEOs, we often have hunches about what factors influence rankings. Maybe you’ve noticed that pages with more backlinks tend to rank higher or that faster-loading sites seem to perform better in search results.
Today, we will look at mathematical tools that can help us validate (or sometimes challenge) these hunches. By the end of this article, you’ll see how these tools will help you separate SEO fact from fiction and boost your confidence in recommending strategies.
The value of applied mathematics in SEO
In the 1985 study “Usefulness of Analogous Solutions for Solving Algebra Word Problems,” researchers found that students often struggled to apply mathematical concepts to similar problems, let alone to real-life situations where these concepts could be beneficial.
This difficulty arises because these concepts are typically learned in isolation. By seeing how these concepts are applied in specific, real-life contexts, students can begin to recognize more opportunities to use them practically.
Today, by examining these tools in the context of SEO, we can start to identify other SEO scenarios that may benefit from applying mathematical concepts.
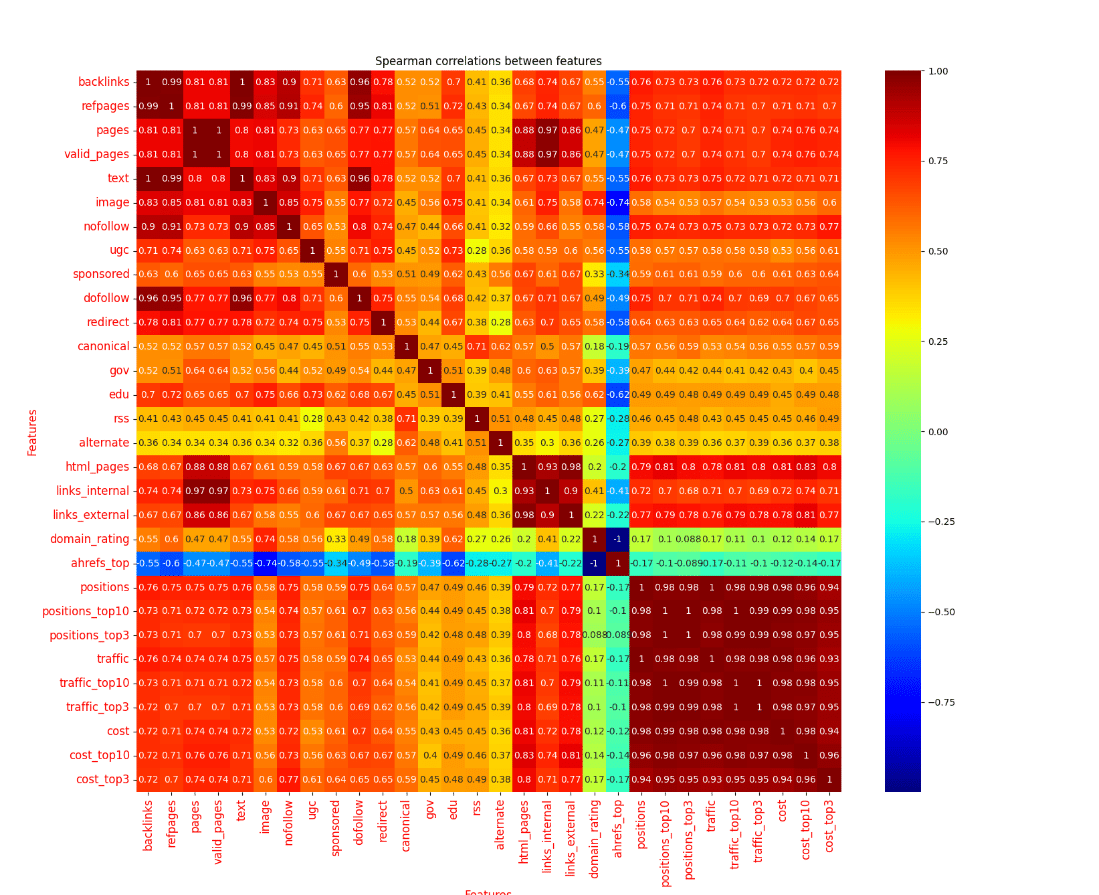
At my agency, we apply correlation analysis in several critical areas:
- The role of quality vs. quantity of referring domains in a given industry.
- The relationship between content and traffic. Is the quantity of content important in an industry?
- The importance of various ranking factors in specific SERP result pages. How important are referring domains to a specific result?
The promise and limitations of correlation analysis in SEO
If we are confident that the Google algorithm has certain ranking features, could we just use correlation analysis of search results to see their influence?
Like most SEO questions, the answer is “it depends.”
Identifying the role of ranking factors and their importance for a SERP is tricky because different ranking factors may not correspond to rankings in a linear or consistently increasing/decreasing way.
For example, consider the impact of page load speed on rankings. A website might see significant ranking improvements when reducing load time from 10 seconds to three seconds, but further improvements from three seconds to one second might yield diminishing returns.
In this case, the relationship between page speed and rankings isn’t linear — there’s a threshold where the impact becomes less pronounced, making it challenging to accurately assess its importance using simple correlation methods.
Before we dive into analyzing specific ranking factors for a SERP, we need to understand the basics of correlation and which method would give us the best results and for which ranking factors. You’ll quickly learn that even though we use mathematics, domain expertise and our expectations about data play a critical role in using mathematics effectively.
Dig deeper: How research on learning can help you understand advanced SEO concepts
So, what is correlation? Let’s go over the two most popular strategies.
Pearson correlation in SEO
Pearson correlation looks for straight-line relationships between two factors. In SEO, this might be useful for factors that tend to increase or decrease steadily with rankings.
Example: Let’s look at the relationship between content length and search engine rankings for a specific keyword.
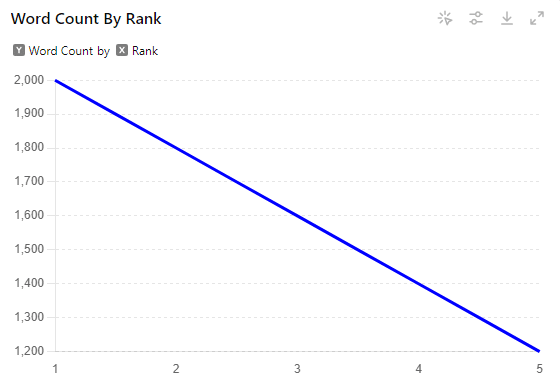
- Rank 1: 2000 words
- Rank 2: 1800 words
- Rank 3: 1600 words
- Rank 4: 1400 words
- Rank 5: 1200 words
Run Python code
import numpy as np
from scipy.stats import pearsonr
# Data
ranks = [1, 2, 3, 4, 5]
word_counts = [2000, 1800, 1600, 1400, 1200]
# Calculate Pearson correlation
correlation, p_value = pearsonr(ranks, word_counts)
print(f"Pearson correlation coefficient: {correlation}")
print(f"P-value: {p_value}")In this example, we see a perfect Pearson correlation. As the content length decreases, the ranking position steadily increases (gets worse). Each drop of 200 words corresponds to a drop of one ranking position.
(In mathematical terms, this would be a perfect negative linear correlation with a value of -1.)
However, real SEO data is rarely this perfect. If the page at Rank 3 had 1,750 words instead of 1,600, we’d still have a strong correlation, but it wouldn’t be perfect.

Pearson correlation in SEO is most useful when we expect a factor to have a consistent, linear relationship with rankings.
Useful tip on statistical significance
The “30 rule” for Pearson correlation suggests that for a correlation to be statistically significant, a sample size of at least 30 is typically needed.
This is based on the Central Limit Theorem, which states that with a sufficiently large sample size (n ≥ 30), the sampling distribution of the correlation coefficient will be approximately normally distributed, allowing for more reliable and valid significance testing.
Spearman correlation in SEO
Spearman correlation is often more useful in SEO because it examines whether one factor tends to increase as another increases (or decreases), even if the relationship isn’t perfectly steady. The beauty of Spearman is that it’s just a Pearson correlation on ranked data.
Example: Let’s look at the relationship between a page’s Ahrefs Domain Rating (DR) and its ranking for a specific keyword.
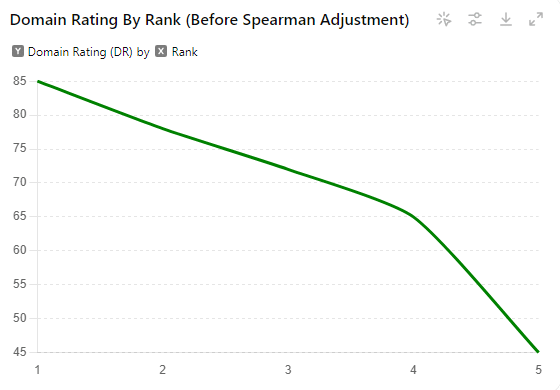
- Rank 1: DR 85
- Rank 2: DR 78
- Rank 3: DR 72
- Rank 4: DR 65
- Rank 5: DR 45
Now, let’s convert this to ranked data:
Step 1: Rank the DR values (highest to lowest):
- 85 (Rank 1)
- 78 (Rank 2)
- 72 (Rank 3)
- 65 (Rank 4)
- 45 (Rank 5)
Step 2: Pair the DR ranks with the SERP ranks:
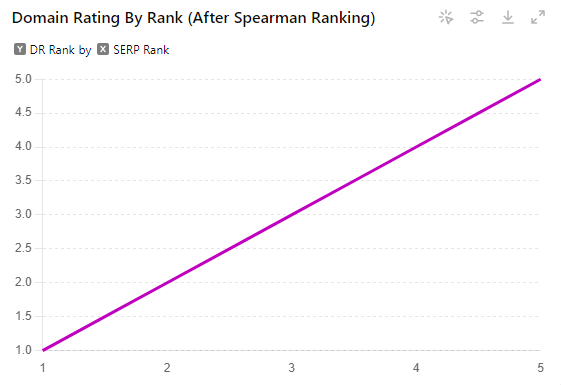
- SERP Rank 1: DR Rank 1
- SERP Rank 2: DR Rank 2
- SERP Rank 3: DR Rank 3
- SERP Rank 4: DR Rank 4
- SERP Rank 5: DR Rank 5
Run Python code
from scipy.stats import spearmanr
# Data
serp_ranks = [1, 2, 3, 4, 5]
dr_ranks = [1, 2, 3, 4, 5]
# Calculate Spearman correlation
spearman_correlation, spearman_p_value = spearmanr(serp_ranks, dr_ranks)
print(f"Spearman correlation coefficient: {spearman_correlation}")
print(f"P-value: {spearman_p_value}")In this case, we end up with a perfect Spearman correlation, even though the original data wasn’t perfectly linear. The Spearman correlation looks at the relationship between these ranks, rather than the raw values.
Here’s why this is powerful: Even if the original DR values were wildly different (say, 1000, 500, 200, 100, 50), as long as they maintained the same order relative to the SERP rankings, the Spearman correlation would be the same.
This approach helps smooth out non-linear relationships and reduces the impact of outliers. In SEO, where many factors don’t have a perfectly linear relationship with rankings, Spearman correlation often gives us a clearer picture of the general trends.
(In technical terms, Spearman correlation looks at the monotonic relationship between variables using ranked data rather than raw values.)
Using this ranking method, Spearman correlation can capture trends that Pearson might miss, making it valuable in our SEO analysis toolkit.
Applying correlation to SEO ranking factors
With correlation, we can begin to think through a basic ranking heuristic for a given search result. For example, let’s imagine a basic formula like this:
- Ranking = w1 * (Referring Domains) + w2 * (Content Length) + w3 * (Site Speed) + … (see our formula based off the recent Google leak).
We can start making educated guesses about the weights (w1, w2, w3, etc.) of these factors based on correlation analysis.
The multitude of ranking factors
Google’s algorithm is incredibly complex, with hundreds of ranking factors at play. As SEOs, we often find ourselves trying to decipher which of these factors are the most crucial.
Over time, through a combination of experience, testing and official Google statements, we typically develop a list of 10-20 factors that we believe are the most impactful.
This list might include elements like:
- Content quality and relevance.
- Backlink profile (quantity and quality).
- User experience signals.
- Page speed.
- Mobile-friendliness.
- Keyword usage and optimization.
- Content freshness.
- SSL security.
- Schema markup.
While this list isn’t exhaustive, it gives us a starting point for our correlation analysis.
Types of ranking factors and what we’d expect
Let’s dive deeper into how different types of ranking factors might behave in our analysis.
Increasing factors
These are factors where we generally expect that more is better. For example, with referring domains, we’d typically expect that sites with more high-quality backlinks would rank higher.
If this factor is significant, we’d see a strong negative correlation between the number of referring domains and ranking position (remember, lower ranking numbers are better).
- Expected correlation: As the number of referring domains increases, ranking position decreases (improves).
Linear ranking factors
These factors tend to have a more straightforward relationship with rankings. Content length could be an example here. If it’s a significant factor, we might see a consistent relationship where longer content correlates with better rankings, up to a point.
- Expected correlation: As content length increases, ranking position decreases (improves) in a relatively consistent manner.
Decreasing ranking relationships
These are factors where lower values are generally better. Site speed is a classic example. We’d expect faster-loading sites to rank higher.
- Expected correlation: As page load time decreases, ranking position decreases (improves).
Binary ranking factors
These are yes/no factors, like whether a site has SSL or not. For these, we might look at the proportion of top-ranking sites that have the factor compared to lower-ranking sites.
- Expected pattern: A higher proportion of top-ranking sites would have the factor compared to lower-ranking sites.
Threshold-based and non-linear factors
These are perhaps the trickiest to analyze with simple correlation. Keyword density is a good example. If it is too little, the page might not be seen as relevant. Too much and it might be seen as keyword stuffing.
- Expected pattern: This is where we might see an “upside-down parabola” shape, which we’ll discuss more in the next section.
The difficulties of using correlations
While correlation analysis can be incredibly useful, it comes with several challenges that are crucial to understand.
Factors in isolation vs. in tandem
When we examine ranking factors individually, we risk overlooking important interactions between them.
For instance, consider a website with high-quality content but fewer backlinks. It might still outrank a site with more backlinks but lower content quality.
This highlights the necessity of looking at multiple factors together to get a true picture of what influences rankings.
Example of Google Ranking factors in parallel
Imagine you are evaluating the impact of various ranking factors on your website’s performance.
Let’s say you consider content quality, backlink quantity and mobile-friendliness. While each of these factors individually contributes to your ranking, their combined effect is what truly matters.
A website that excels in content quality and mobile-friendliness but has fewer backlinks might still perform well due to the synergy between high-quality content and a user-friendly mobile experience.
Overpowering ranking factors
It’s also crucial to understand that some ranking factors can greatly overpower others.
For example, if a website has an exceptionally high number of authoritative backlinks, this might significantly boost its rankings even if its content quality is moderate.
This dominance can make it challenging to see the impact of smaller factors, such as page load speed. Because the effect of the stronger factor overshadows the weaker one, a site with excellent backlinks might not need to focus as heavily on improving load speed to see ranking improvements.
Quadratic nonlinear relationships
Some factors have what we call an “upside-down parabola” shape. Keyword usage is a perfect example. Let’s say we’re analyzing the keyword density of “best running shoes” in product reviews:
- 0% density: The page likely won’t rank at all for the term.
- 0.5% density: This might be ideal, helping the page rank well.
- 1% density: Still good, maybe ranking slightly lower.
- 2% density: Starting to look like keyword stuffing, rankings drop.
- 5% density: Likely seen as spam, rankings plummet.
If we plotted this, we’d see an upside-down U shape, with the best rankings in the middle and worse rankings at both extremes.
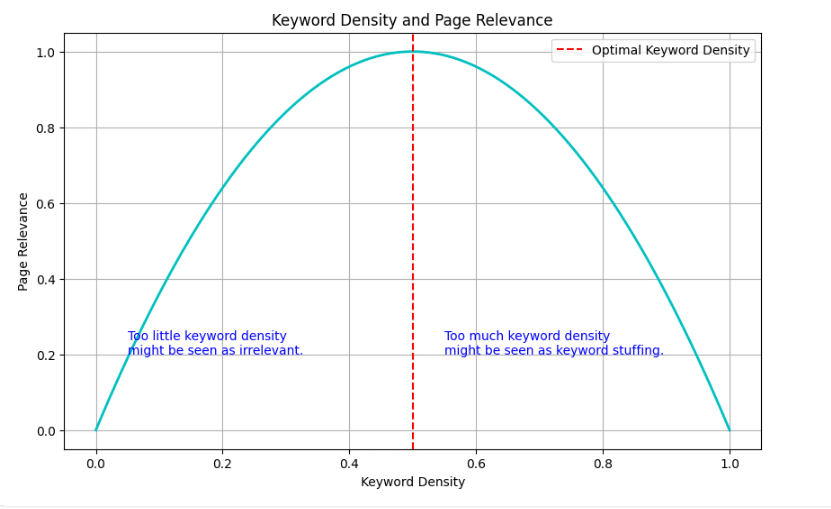
Analyzing non-linear factors
To analyze factors like this, we might need to get creative. Instead of looking at the raw keyword density, we could:
- Look for the min and max frequency in the top-ranking results and correlate that instead. This gives us a “sweet spot” range.
- Use a quadratic regression instead of linear correlation, which can capture this parabolic relationship.
- Transform the data. For example, we could calculate the absolute difference from the “ideal” density (say, 0.5%) and correlate that with rankings. This would show that being close to the ideal in either direction correlates with better rankings.
Other issues
Confounding variables: Sometimes, what looks like a correlation might be explained by another factor entirely. For instance, we might see a correlation between word count and rankings, but this could be because longer content tends to be more comprehensive and valuable, not because Google has a “word count” factor.
Causation vs. correlation: Just because two things are correlated doesn’t mean one causes the other. For example, we might see a correlation between the number of social shares and rankings. But this doesn’t necessarily mean social shares directly influence rankings; it could be that great content both ranks well and gets shared more.
Sample size and variability: When we’re looking at a single SERP, we’re dealing with a small sample size, which can lead to misleading conclusions. It’s often better to analyze patterns across multiple SERPs in the same niche.
Time lag: Some factors might have a delayed effect on rankings. For instance, new backlinks might take time to influence rankings, making it hard to spot the correlation if we’re looking at current backlink numbers and current rankings.
By understanding these complexities, we can use correlation analysis more effectively, combining it with other analytical tools and our SEO expertise to draw meaningful conclusions about ranking factors.
Additional hurdles in correlation analysis for SEO
Unknown algorithm weights: Without knowing the exact weights Google assigns to different factors, our correlation analysis may not accurately reflect their true importance.
Relevance effects: Tools like BM25, named entity recognition and TF-IDF attempt to quantify relevance, but how these interact with other factors like backlinks can be complex and difficult to capture in a simple correlation analysis.
Domain-level metrics: The leaked information suggests that overall domain metrics may be factored into the scoring algorithm. Since we’re only looking at the SERP itself and individual page factors, these domain-level influences act as a black box that could dramatically change rankings.
Spurious correlations: It’s important to be aware that correlation does not imply causation. Some factors may show strong correlations but not actually be causal in determining rankings.
Correlated factors: Many SEO factors are not independent of each other, making it difficult to isolate their individual effects through correlation analysis alone.
These hurdles underscore why domain knowledge and expertise are crucial. As the person conducting the analysis, you need to have some idea of what you would expect these factors to do to be able to interpret the results meaningfully.
What is a strong correlation in a SERP result?
Obviously a .99 correlation is great, but given the interplay of so many variables when should we really take notice of a ranking factor and its importance?
In the messy world of SEO, a 0.99 (or -.99) correlation would be suspiciously high. More realistically, we should start paying attention to correlations around 0.2 to 0.5, especially if they’re consistent across multiple analyses.
As a result, when correlations emerge in SEO analysis, they tend to be much smaller than we might expect in more straightforward relationships. This doesn’t diminish their importance, however.
Even these smaller correlations can provide valuable insights into the factors influencing search rankings, especially when viewed as part of a broader pattern rather than in isolation.
Here’s when you should really take notice:
- Repeatability: If you’re seeing similar correlations for a factor across different keywords, time periods, or industries, it’s more likely to be important.
- Alignment with SEO knowledge: If the correlation aligns with what we know about SEO best practices or Google’s stated preferences, it’s more likely to be meaningful.
Where can correlation help beyond our SEO intuitions?
Now, you might be thinking, “This is all well and good, but how does it actually help me in the real world? Could’t I just eyeball the search results and see the factors that matter?”
Great question! Here are some practical applications where correlation analysis can give us additional insights that go beyond our gut feelings.
- Ruling out the influence of some factors: Sometimes, what we think matters… doesn’t. For example, you might believe that using exact-match keywords in H2 tags is crucial for ranking. But when you run a correlation analysis, you find no significant relationship between H2 keyword usage and rankings. This doesn’t mean H2 tags are useless, but it suggests they might not be as important as you thought.
- Unveiling industry-specific ranking factors.
- Prioritizing SEO efforts.
- Measuring the impact of algorithm updates: If you monitor how correlations change with algorithm updates, it can help point out which underlying factors may have changed in the update.
Advanced strategies and future directions
While correlation analysis is a useful first step in understanding ranking factors, more advanced techniques can be applied that can better handle the multivariate nature of ranking factors and the many different types of relationships ranking factors may have with scoring.
- Regression analysis: This can help determine the relative importance of multiple factors simultaneously.
- Decision trees: These can capture non-linear relationships and interactions between factors.
- Machine learning at scale: Combining correlation techniques with machine learning can reveal complex patterns across large datasets.
Using correlation analysis to inform your SEO strategy
Correlation analysis can be a powerful tool for SEOs seeking to understand the relative importance of various ranking factors. However, it’s crucial to approach this analysis with a solid understanding of statistical concepts, awareness of the limitations and strong domain expertise.
By combining correlation analysis with other advanced techniques and always grounding our interpretations in SEO best practices, we can gain valuable insights to inform our strategies and decisions.
Dig deeper: Analyze content publishing velocity with this Python script
source https://searchengineland.com/seo-decision-making-correlation-analysis-443925


0 Comments